(注: 只是个人半年前的一些研究总结,在此仅此记录。)
1 背景资料:
推荐系统基于两种策略:
a) 基于内容的过滤(Content-based filtering)
b) 协同过滤 (Collaborative filtering) (CF)
模型:
) 内容过滤需要根据内容创建模板,诸如用物品的title,名字。等等。
当然也可以根据用户建立模板。用户的画像等等。
b) 基于协同过滤。会从历史记录中,找出item-User之间的关系,并建立相关模型。
差异:
从某些场景来看,内容过滤更为优秀,比如一个新用户(没有任何的历史)。或是一个新商品,没有任何的关联数据。这个时候基于Content-Based的过滤,显得更恰当。
然而,在大多数的场景下,协同过滤会变得更为优秀。原因在于,他更充分的考虑到User-Item之间的关系。当然,该方法也使用的更为广泛。
2 协同过滤的集中分类
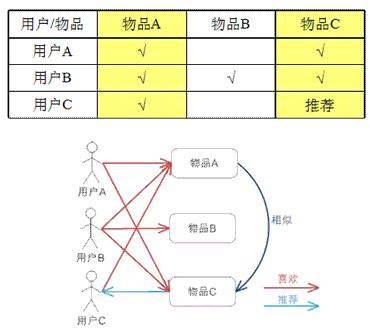
2.1 基于物品的协同过滤
构建 Item -> User的向量: V(I->U)
计算 各个Verctor之间的相似度
直观理解: 把和你之前喜欢的物品近似的物品推荐给你
2.2 基于用户的的协同过滤
构建 User -> Item的向量: V(U->I)
计算 各个Verctor之间的相似度
直观理解:把就是把与你有相同爱好的用户所喜欢的物品,推荐给你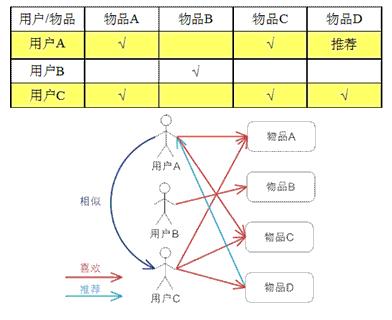
2.3 比Item-CF和User-CF
ItemCF: 多样性不足 (覆盖率)
UserItem: 长尾性不足。
综合:兴趣点不同。
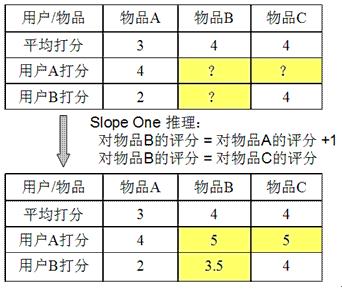
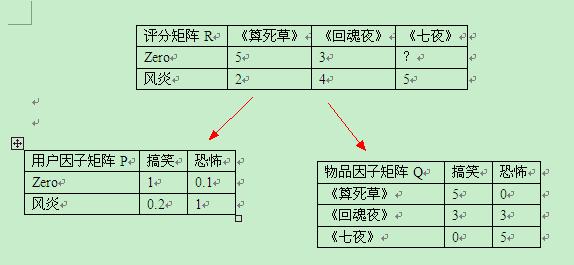
2.4 于评分的协同过滤 (Slope One)
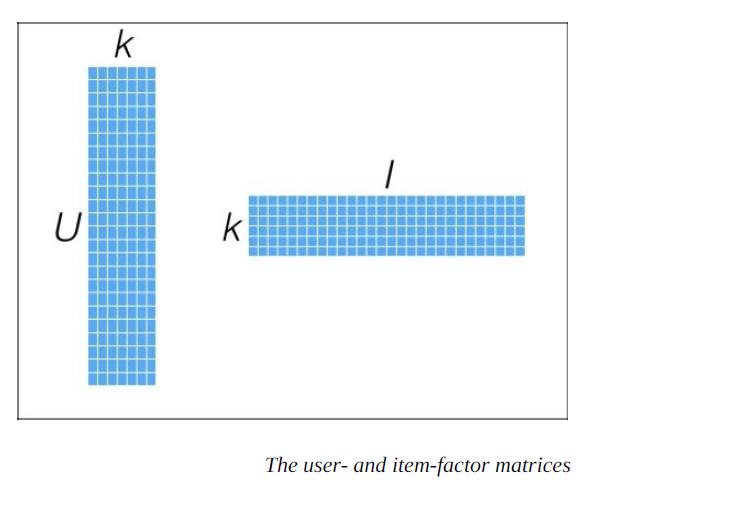
3 SVD与协同过滤
3.1 传统的SVD
SVD (singular value decomposition) 奇异值分解。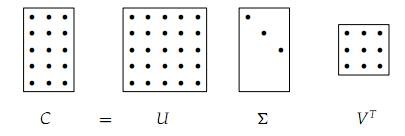
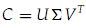
低阶近似:
- 给定一个矩阵C,对其奇异值分解:
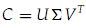
- 构造
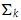 ,它是将
,它是将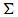 的第k+1行至M行设为零,也就是把
的第k+1行至M行设为零,也就是把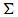 的最小的r-k个(the r-k smallest)奇异值设为零。
的最小的r-k个(the r-k smallest)奇异值设为零。 - 计算
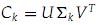
特征值数值的大小对矩阵-向量相乘影响的大小成正比,而奇异值和特征值也是正比关系,因此这里选取数值最小的r-k个特征值设为零合乎情理,即我们所希望的C-Ck尽可能的小
3.2 传统的SVD能否应用于协同过滤(基于评分)的模型?
首先有几个问题 :
1. 传统的SVD对于高维稀疏矩阵实惠丢失一些特征信息。
2. 当矩阵不完全时,SVD是无法定义的。 (完全我的理解是有些值是没有定义 ,缺省,用latent factor 可以解)
3. 如果只对已知的信息求解,会非常容易过度拟合。 (我的理解:没有加入Lambda*规则化)
另外,要计算SVD的特征值,对于高维数据来说,也是代价巨大的。
3.3 SVD因式分解,实现协同过滤
公式1 : 因式分解(plain)
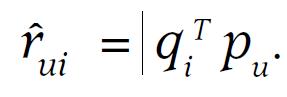
设定有那么一个转换,能够将已知的评分Matrix分解成两个Factor矩阵相乘。一个和Item相关,一个和User相关
公式2: 规则化*Lambda (L2)
规则化的目的,是防止过度拟合。
其中Lambda太大,容易低拟合。Lambda太小,容易过拟合。
(这里的Lambda在Spark中需要根据实际的数据样本分布,维度的大小调整)
当然,这里用的是L2拟合。(区别于L1),L2是二次函数拟合。
(L2拟合的目的是使得W的元素很小,接近于0,但不等于0,会使得模型简单。这样使得个别值对全局的印象降低,越简单的模型越不容易产生过拟合)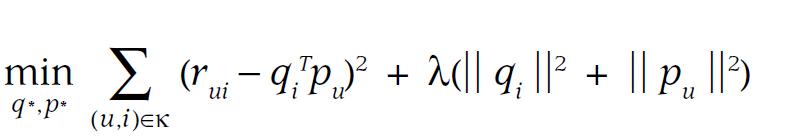
公式3 基线公式(偏好)
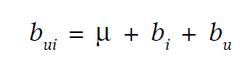
其中:
U是所有投票的均值
bu是用户打分相对于均值的偏差。
bi 是该item被打分相对于均值的偏差
(该公式是ALS算法的最原始形态)
公式4 单个打分
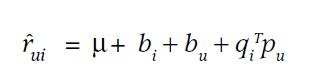
该公式是由 (公式1 ) + (公式3) 推得
单条记录的打分
公式5 整体打分求最小化
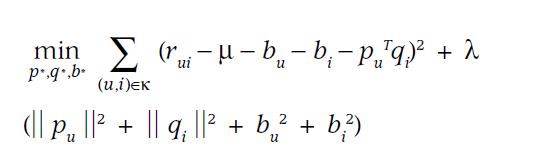
由以上同时推得。
公式6 外部数据
为了避免冷启动问题,需要加入外部数据。否则会导致新用户的数据非常少。
那么外部数据时什么? 是基于该用户的一些其他特征(画像)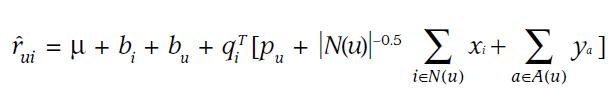
公式7 动态时间
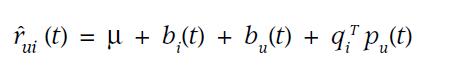
将时间作为权重考虑进去。
目的是:用户的倾向会随着时间而发生变化,使得更好的捕捉最新的趋势。
公式8 自信度(Implicit , latent factor)
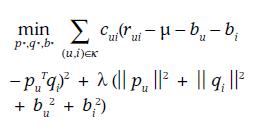
该公式和之后Spark中使用trainImplict的理论基本一致。
输入矩阵是不同的Confidence Levels
几种优化结果:
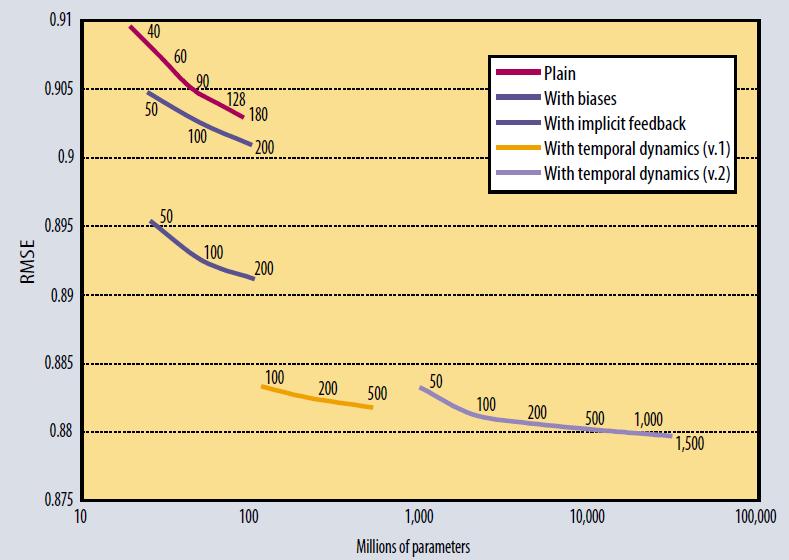
4 Implict Feedback
显然,如果用户对于物品已经有的评分,这些数据称之为explicit。
但是,有些数据,诸如物品的点击数等,这些并不能直接反应用户对该物品的评分。只是表明了一种倾向,但是,究竟是正向的倾向,还是负向的倾向,是不确定的。
Implicit feedback 的数据和 explicit data的数据是非常不同的:
a) 矩阵是完整定义了的。 (explicit的数据会有Miss)
b) 没有负向的反馈。 (没有明显的倾向)
c) 在0值的时候,是没有交互定义的。
d) 对于这部分数据,必然没有十足的把握(相对于显示的评分,信心不足)
e) 当然,用标准的SVD显然是无法求得这种关系的。
以下几张图可以一目了然其计算法则: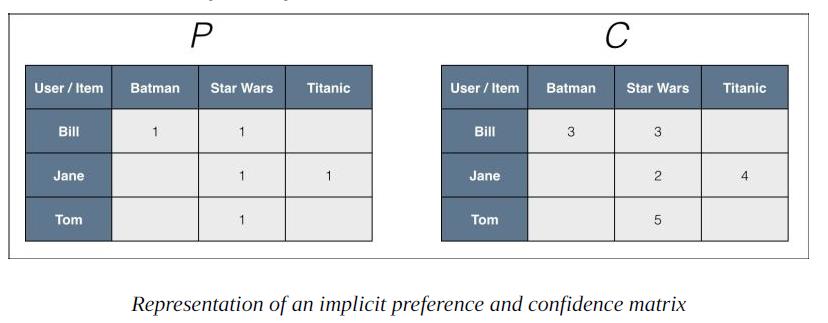
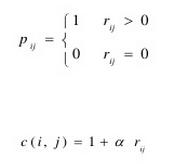
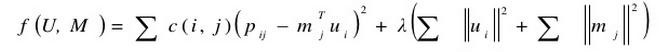
但,Collaborative Filtering for Implicit Feedback Dataset 这篇论文暂时没有搜索到原文。
只能通过代码来分析其计算公式。
|
|
所以,在Spark中,参数为alpha的值,是用来调节自信率的。
5 ALS和SGD
即便我们已经有了上述的许多公式,我们如何求解?
5.1 随机梯度下降(SGD)
Stochastic Gradient Descent
在数学上,我们知道。 一个符合convex的函数是可以求得最小值的。
这样一来,我们就有了梯度下降的求解方法,其梯度下降的速度,取决于convex函数的凸性强不强。
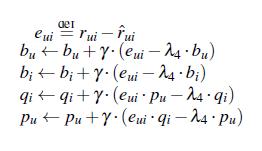
这就是梯度下降的迭代公式,当然,该算法已经应用于Mahout中实现。
5.2 ALS算法
Alternating Least Squares (交替最小方差算法)
该算法有两个优点:
1) ALS更容易并行化。
2) ALS对处理隐式数据更方便。
根据5.1的公式中: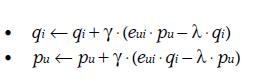
这两共公式各自有两个变量,我们可以固定其中一个变量,这样使得其编程一个二次函数,能够被最优化求解。
而ALS就是不断的交替固定Pu和Qi,然后求解另一个变量的最优值。
当然,通常来说,SGD会比ALS更加简单和快速,但是ALS的并行性比较好。如果矩阵是稀疏矩阵,那么ALS更有优势
6 算法的检验
RMSE/MSE/MAPK
待续….
7 Reference
spark,als-ws 基础
http://www2.research.att.com/~volinsky/papers/ieeecomputer.pdf
协同过滤部分:
http://www.ibm.com/developerworks/cn/web/1103_zhaoct_recommstudy2/index.html
http://www.52ml.net/297.html
svd 部分:
http://blog.csdn.net/wangran51/article/details/7408414
http://blog.csdn.net/qianhen123/article/details/40077873
规则化:
http://blog.csdn.net/u012162613/article/details/44261657
Latent-factor-models
http://www.slideshare.net/sscdotopen/latent-factor-models-for-collaborative-filtering
作者:3h_william
联系: https://github.com/3h-william
出处:http://3h-william.github.io